Latest Blogs
Click here to check out more blogs.
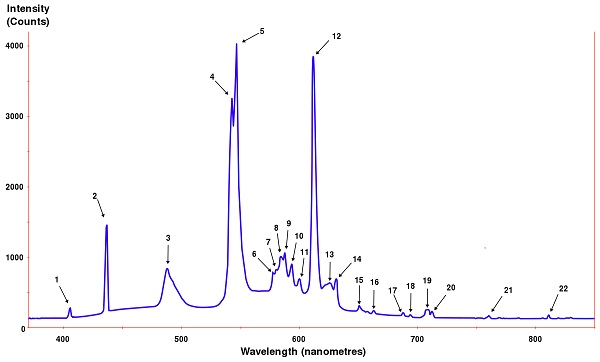
Re-optimizing aLIGO RF filter
Electronics
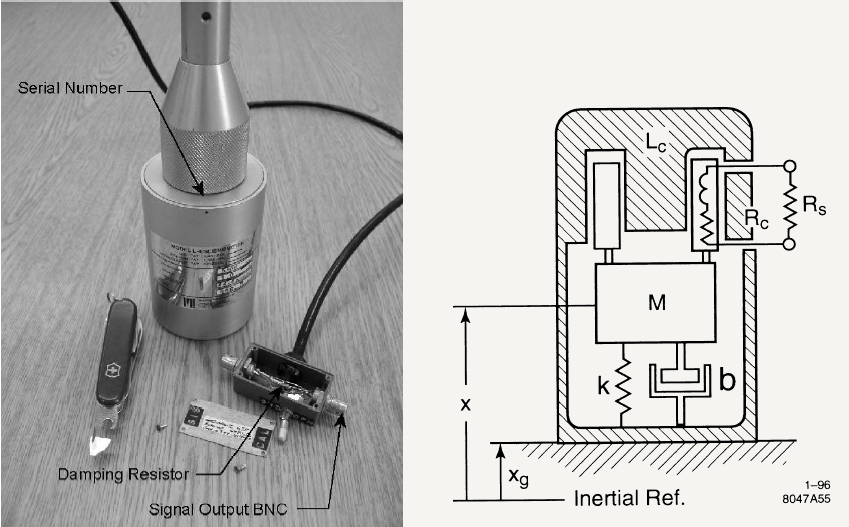
L4C Seismometer transfer function
Electronics
Silicon Based Quantum Computer
Quantum Computation
Solenoid plungers
Electromagnetism
Musings on the Weibull distribution
Reliability
Rice distribution
Statistics
An analysis of aLIGO PD circuit
Electronics
The Legendre Transform
Classical Mechanics
Decoherence due to phonons
Quantum
Computing joint confidence intervals
Statistics
LIGO Laser modulation
Electronics
Grover’s Algorithm
Quantum Computation
Shor’s Algorithm
Quantum Computation
Superconducting Bits
Quantum Computation
Getting Started with Qiskit
Quantum Computation
Parametric Amplifier
Math
Johnson Noise
Math
Adding two Weibull random numbers
Statistics
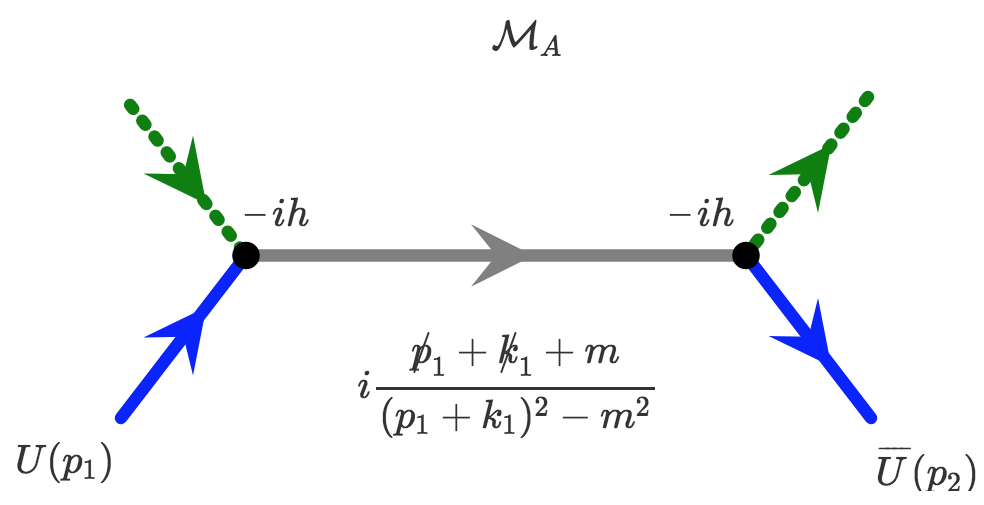
Scattering fermions and scalars
Quantum Field Theory
Installing and Using GetDP on macOS
Numerical Methods
\(2-\)D Quantum Oscillator
Quantum
A refresher on statistical mechanics
Thermodynamics
Biot-Savart Law
Electromagnetism
Inductance of a Wire Pair with Neumann’s Method
Electromagnetism
Inductance of a Wire Pair
Electromagnetism
Self-Inductance of a Wire
Electromagnetism
Magnetic Dipole
Electromagnetism
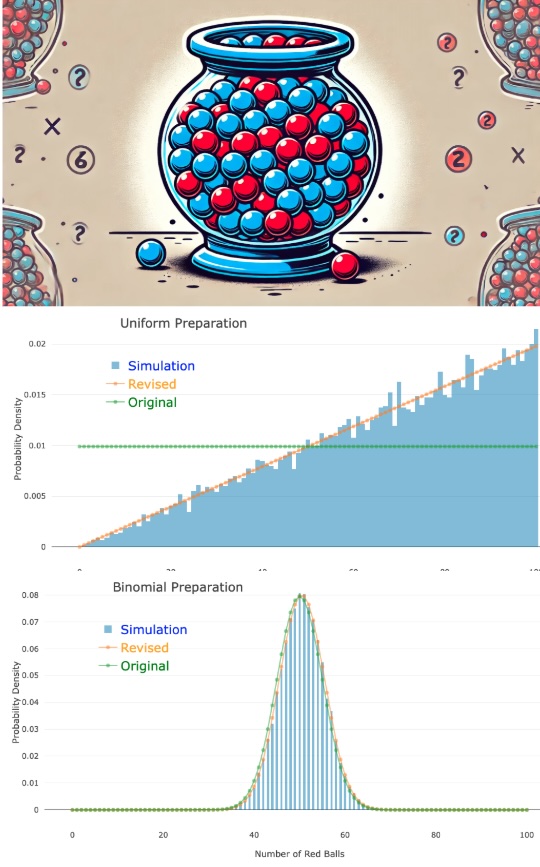
Red balls, Green Balls
Statistics
Fabry-Perot Cavity
Optics
Renewal Processes
Statistics
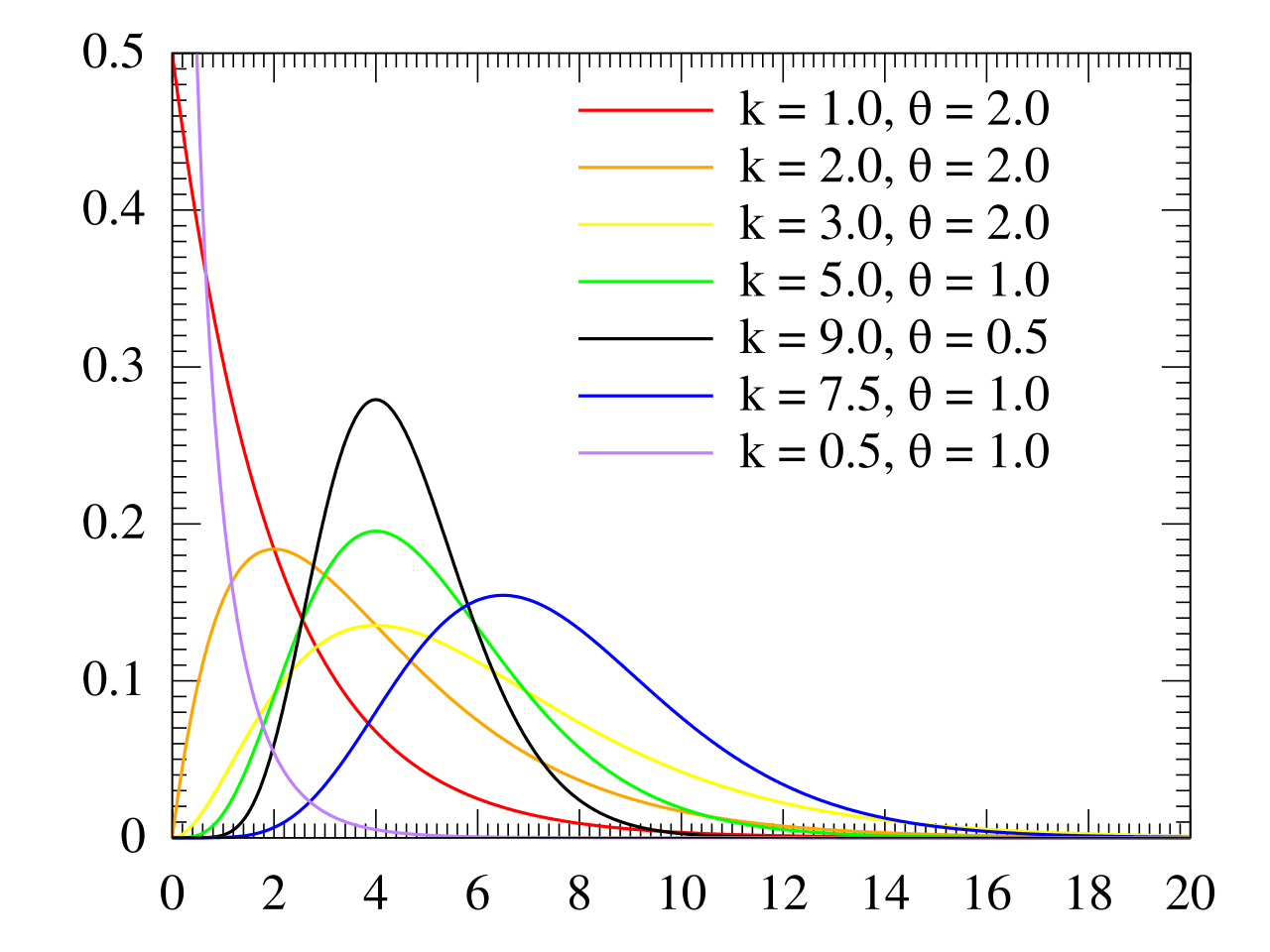
Musings on the Gamma Distribution
Statistics
Musings on the Exponential Distribution
Statistics
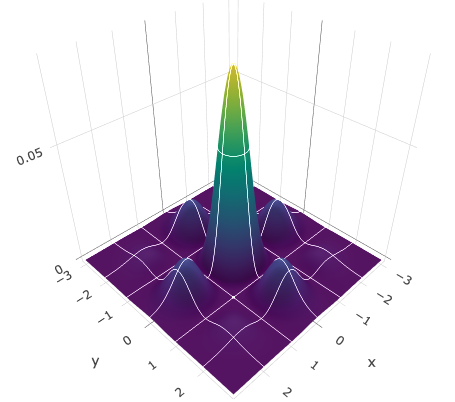
Diffraction
Optics
Coil calculations
Electromagnetism
Abrikosov-Nielsen-Olesen flux tubes
Superconductivity
Canonical Transformations
Classical Mechanics
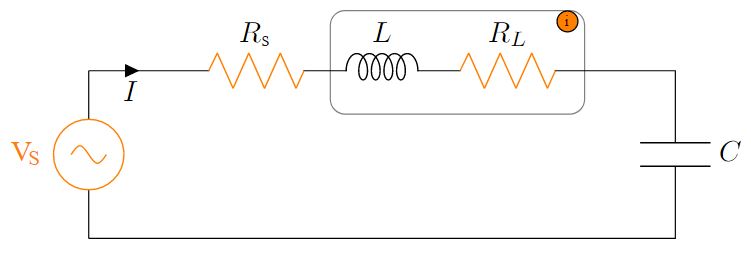
Real coils are not purely imaginary
Electronics
An SNR analysis of aLIGO circuit
Electronics
Quantum Harmonic Oscillator
Quantum
A crash course on JFETs
Electronics
Noise analysis of OPAMPs
Electronics
Lagrange Multipliers
Math
Pandemic, home-schooling, and dragons: 2021 Edition
Short Stories
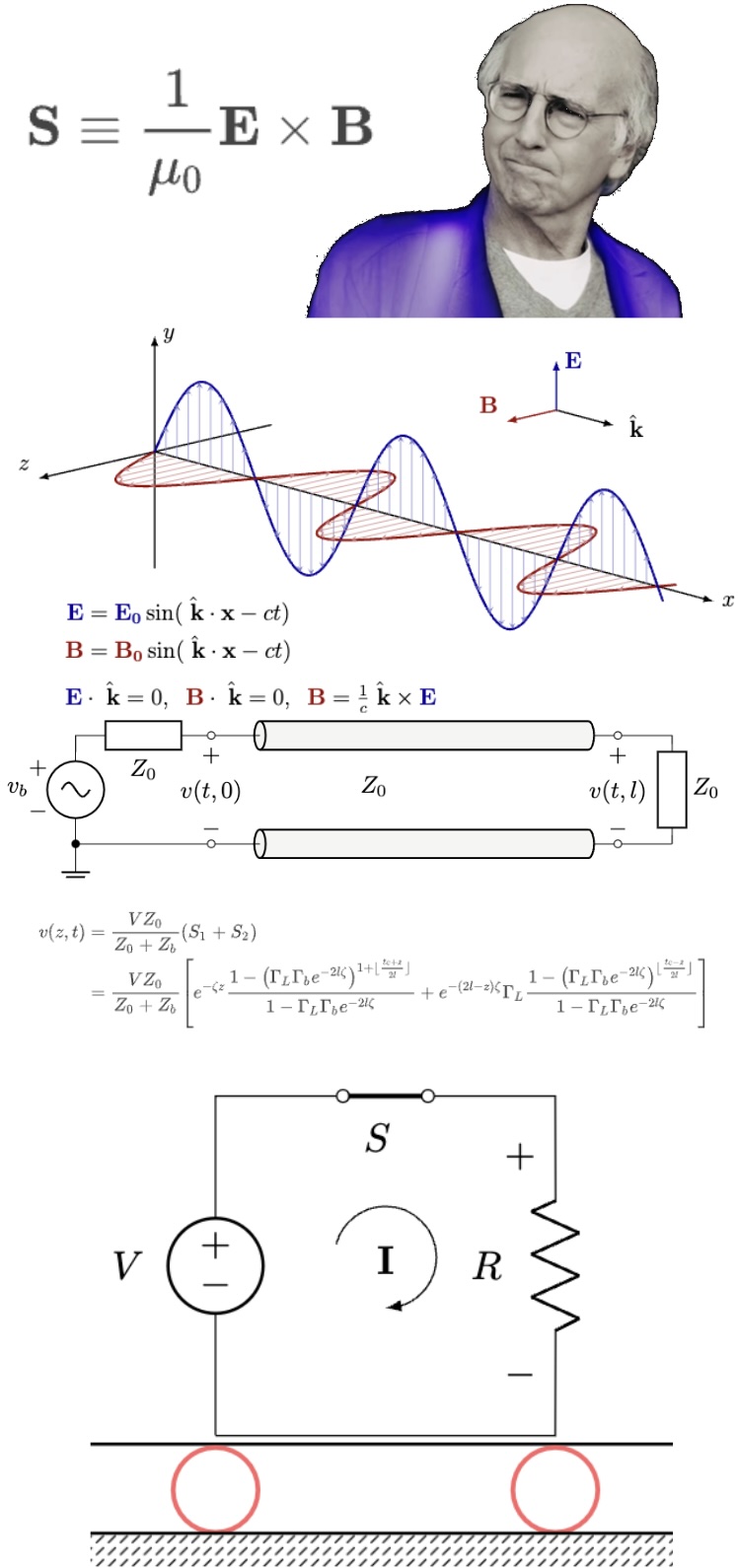
Curl your Poynting vector
Electromagnetism
The math of low pass filtered PWM
Electronics
Hacking into a wheelchair controller
Electronics
There is no such thing as farmer’s wife
Random Rants
Pandemic, home-schooling, and dragons
Short Stories
Thomas-Reiche-Kuhn sum rules
Quantum
Filter Matching
Statistics
Hydrogen Atom in Magnetic Field
Quantum
Nuclear Magnetic Resonance Based Quantum computer
Quantum Computation
A romantic walk under rain and partial derivatives
Short Stories
No matching items